News Message
凸优化笔记11:对偶问题
- by show 2021-02-15
1. 拉格朗日函数
考虑凸优化问题
![[公式]](/images/download/1613377606198_37693.png)
假设 ![[公式]](/images/download/1613377606557_69420.png) ,定义域为
,定义域为 ![[公式]](/images/download/1613377606592_63545.png) ,最优解为
,最优解为 ![[公式]](/images/download/1613377606625_49218.png) 。
。
我们定义拉格朗日函数(Lagrangian) 为 ![[公式]](/images/download/1613377606670_13171.png) ,
,![[公式]](/images/download/1613377606713_89503.png)
![[公式]](/images/download/1613377606755_57529.png)
再取下确界得到拉格朗日对偶函数(Lagrange dual function) ![[公式]](/images/download/1613377606838_43630.png)
![[公式]](/images/download/1613377606875_88205.png)
这个拉格朗日对偶函数可不得了啦!他有两个很重要的性质:
![[公式]](/images/download/1613377606944_64495.png) 是凹函数(不论原问题是否为凸问题)
是凹函数(不论原问题是否为凸问题)- 如果
![[公式]](/images/download/1613377606979_12105.png) ,那么
,那么 ![[公式]](/images/download/1613377607016_72455.png) (对任意
(对任意 ![[公式]](/images/download/1613377607050_37068.png) 都成立)
都成立)
Remarks:上面两个性质为什么重要呢?首先由于 ![[公式]](/images/download/1613377607098_33352.png) ,这可以给出原问题最优解的一个不平凡下界,这意味着如果原问题很难求解的时候,我们可以转变思路,求解一个新的优化问题:
,这可以给出原问题最优解的一个不平凡下界,这意味着如果原问题很难求解的时候,我们可以转变思路,求解一个新的优化问题:
![[公式]](/images/download/1613377607136_16340.png)
另一方面,由于不论原函数是否为凸优化问题,新的问题都是凸的,因此可以方便求解。下面举几个例子。
例子 1:原问题为
![[公式]](/images/download/1613377607199_37887.png)
那么可以很容易得到拉格朗日函数为 ![[公式]](/images/download/1613377607268_34516.png) ,对偶函数为
,对偶函数为 ![[公式]](/images/download/1613377607319_67732.png) ,也即
,也即
![[公式]](/images/download/1613377607379_18419.png) 。
。
例子 2:标准形式的线性规划(LP)
![[公式]](/images/download/1613377607410_88273.png)
按照定义容易得到对偶问题为
![[公式]](/images/download/1613377607473_17048.png)
例子 3:原问题为最小化范数
![[公式]](/images/download/1613377607540_20113.png)
对偶函数为
![[公式]](/images/download/1613377607594_84784.png)
这个推导过程中用到了共轭函数的知识。实际上上面三个例子都是线性等式约束,这种情况下,我们应用定义推导过程中可以很容易联想到共轭函数。(实际上加上线性不等式约束也可以)
例子 4:(原问题非凸)考虑 Two-way partitioning (不知道怎么翻译了...)
![[公式]](/images/download/1613377607682_95907.png)
对偶函数为
![[公式]](/images/download/1613377607751_78961.png)
于是可以给出原问题最优解的下界为 ![[公式]](/images/download/1613377607860_19930.png) if
if ![[公式]](/images/download/1613377607897_95387.png) 。这个下界是不平凡的,比如可以取
。这个下界是不平凡的,比如可以取 ![[公式]](/images/download/1613377607937_30840.png) ,可以给出
,可以给出 ![[公式]](/images/download/1613377607983_55086.png) 。
。
2. 对偶问题
上面已经多次提到对偶问题(Lagrange dual problem) 了
![[公式]](/images/download/1613377608026_54219.png)
假如对偶问题的最优解为 ![[公式]](/images/download/1613377608089_89994.png) ,那么我们有
,那么我们有 ![[公式]](/images/download/1613377608134_88076.png) 。
。
现在我们当然想知道什么情况下可以取等号,也即 ![[公式]](/images/download/1613377608166_40439.png) ,此时我们只需要求解对偶问题就可以获得原问题的最优解了。在此之前,我们先引入两个概念:强对偶和弱对偶。
,此时我们只需要求解对偶问题就可以获得原问题的最优解了。在此之前,我们先引入两个概念:强对偶和弱对偶。
弱对偶(weak duality):满足 ![[公式]](/images/download/1613377608204_78911.png) ,原问题不论是否为凸,弱对偶总是成立;
,原问题不论是否为凸,弱对偶总是成立;
强对偶(strong duality):满足 ![[公式]](/images/download/1613377608235_89579.png) ,强对偶并不总是成立,如果原问题为凸优化问题,一般情况下都成立。在凸优化问题中,保证强对偶成立的条件为被称为 constraint qualifications。
,强对偶并不总是成立,如果原问题为凸优化问题,一般情况下都成立。在凸优化问题中,保证强对偶成立的条件为被称为 constraint qualifications。
有很多种不同的 constraint qualifications,常用到的一种为 Slater’s constraint qualification(SCQ),其表述为
SCQ:对于凸优化问题
![[公式]](/images/download/1613377608267_67203.png) 如果存在可行解
如果存在可行解 ![[公式]](/images/download/1613377608350_99385.png) ,使得
,使得
![[公式]](/images/download/1613377608381_33145.png) 那么就能保证强对偶性。
那么就能保证强对偶性。
Remarks:
- 由于存在线性等式约束,因此实际定义域可能不存在内点,可以将这一条件放松为相对内点
![[公式]](/images/download/1613377608432_25011.png) ;
; - 如果不等式约束中存在线性不等式,那么他也不必严格小于0。也即如果
![[公式]](/images/download/1613377608463_26788.png) ,则只需要满足
,则只需要满足 ![[公式]](/images/download/1613377608503_53409.png) 即可。
即可。
下面再举几个例子,看一看他们的 SCQ 条件是什么。
例子 1:还是考虑线性规划(LP) 或者二次规划(QP)
![[公式]](/images/download/1613377608536_61744.png)
那么根据 SCQ 可以得到,如果想得到强对偶性,应该有 ![[公式]](/images/download/1613377608615_22478.png) 。
。
例子 2:(原问题非凸) Trust Region Methods
![[公式]](/images/download/1613377608656_90642.png)
其中 ![[公式]](/images/download/1613377608720_97067.png) ,因此原问题不是凸的。他的对偶函数就是
,因此原问题不是凸的。他的对偶函数就是
![[公式]](/images/download/1613377608751_60342.png)
注意如果不满足 ![[公式]](/images/download/1613377608863_71415.png) 或
或 ![[公式]](/images/download/1613377608898_59475.png) ,则
,则 ![[公式]](/images/download/1613377608932_76291.png) 。那么就可以得到对偶问题为
。那么就可以得到对偶问题为
![[公式]](/images/download/1613377608963_13585.png)
也可以等价转换为 SDP
![[公式]](/images/download/1613377609063_86018.png)
Remarks:这里用到了舒尔补(Schur complement)的知识。考虑矩阵
![[公式]](/images/download/1613377609133_89363.png) 其中
其中 ![[公式]](/images/download/1613377609175_11859.png) 。那么有以下及条性质:
。那么有以下及条性质:
![[公式]](/images/download/1613377609222_39247.png)
- 若
![[公式]](/images/download/1613377609263_85887.png) ,则
,则 ![[公式]](/images/download/1613377609295_67997.png)
![[公式]](/images/download/1613377609335_33548.png)
关于第 3 条中的第二个要求 ![[公式]](/images/download/1613377609391_40198.png) ,对
,对 ![[公式]](/images/download/1613377609428_74824.png) 进行奇异值分解,有
进行奇异值分解,有 ![[公式]](/images/download/1613377609454_50699.png) ,那么我们对任意
,那么我们对任意 ![[公式]](/images/download/1613377609490_57255.png) ,有
,有 ![[公式]](/images/download/1613377609519_71702.png) ,而
,而 ![[公式]](/images/download/1613377609575_99337.png) 实际上就是向
实际上就是向 ![[公式]](/images/download/1613377609609_20848.png) 的投影矩阵,因此就要求
的投影矩阵,因此就要求 ![[公式]](/images/download/1613377609677_98194.png) 。
。
3. SCQ 几何解释
前面给出的是 SCQ 的代数描述,那么如何证明呢?另外如何从几何角度直观理解呢?
首先我们可以考虑最简单的优化问题
![[公式]](/images/download/1613377609716_83721.png)
定义集合 ![[公式]](/images/download/1613377609790_40031.png) ,那么对偶函数为
,那么对偶函数为
![[公式]](/images/download/1613377609843_63551.png)
如果我们画出下面这张图,阴影部分就是可行区域 ![[公式]](/images/download/1613377609918_78189.png) ,而
,而 ![[公式]](/images/download/1613377609948_56593.png) 则正好定义了一个支撑超平面,
则正好定义了一个支撑超平面,![[公式]](/images/download/1613377610002_69750.png) 就等于
就等于 ![[公式]](/images/download/1613377610045_87114.png) 轴的交点。通过取不同的
轴的交点。通过取不同的 ![[公式]](/images/download/1613377610075_14004.png) 我们就可以得到不同的支撑超平面,也可以得到不同的
我们就可以得到不同的支撑超平面,也可以得到不同的 ![[公式]](/images/download/1613377610106_73756.png) ,最终会有某一个
,最终会有某一个 ![[公式]](/images/download/1613377610136_12046.png) 对应的是
对应的是 ![[公式]](/images/download/1613377610167_44231.png) 。还需要注意这里的支撑超平面永远不可能是竖直的。
。还需要注意这里的支撑超平面永远不可能是竖直的。
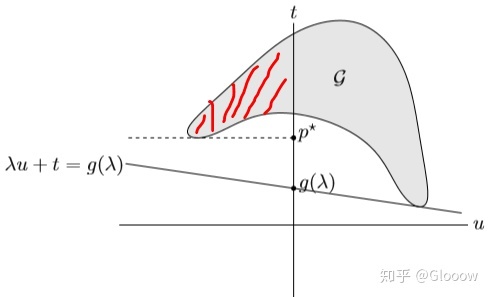
(λ,1)^T 正好定义了一个支撑超平面 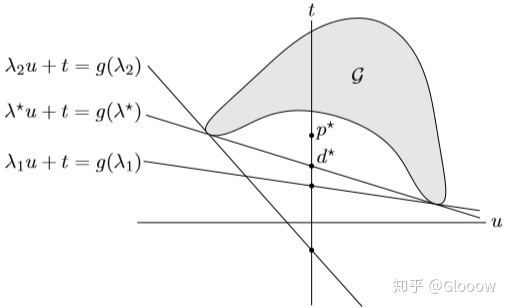
每个 λ 对应一个支撑超平面 那么 ![[公式]](/images/download/1613377610290_32358.png) 体现在哪个点呢?由于对于原优化问题,我们有
体现在哪个点呢?由于对于原优化问题,我们有 ![[公式]](/images/download/1613377610323_83633.png) ,因此体现在这个图里面就是
,因此体现在这个图里面就是 ![[公式]](/images/download/1613377610361_69158.png) ,也就是上面左图当中的红色区域,而
,也就是上面左图当中的红色区域,而 ![[公式]](/images/download/1613377610390_98350.png) 。
。
理解了这张图,我们现在开始证明两件事:
- 证明弱对偶性,也即
![[公式]](/images/download/1613377610431_82168.png) ;
; - 证明强对偶性条件 SCQ。
注:在此之前,我们不妨加入等式约束,也即 ![[公式]](/images/download/1613377610472_63424.png) 。
。
弱对偶性的证明:我们有 ![[公式]](/images/download/1613377610533_99687.png)
![[公式]](/images/download/1613377610567_56890.png)
强对偶性条件 SCQ 的证明:由 ![[公式]](/images/download/1613377610698_13284.png) 可以得到
可以得到
![[公式]](/images/download/1613377610755_99304.png)
这实际上定义了 ![[公式]](/images/download/1613377610820_55605.png) 的一个超平面。特别的有
的一个超平面。特别的有 ![[公式]](/images/download/1613377610846_81934.png) ,因此也有
,因此也有
![[公式]](/images/download/1613377610886_85421.png)
这个不等式可以自然地导出弱对偶性,当“=”成立时则可以导出强对偶性。那么什么时候取等号呢?点 ![[公式]](/images/download/1613377610940_24454.png) 为支撑点的时候!也就是说
为支撑点的时候!也就是说
如果在边界点 ![[公式]](/images/download/1613377610975_48988.png) 处存在一个非竖直的支撑超平面,那么我们就可以找到
处存在一个非竖直的支撑超平面,那么我们就可以找到 ![[公式]](/images/download/1613377611012_90059.png) 使得上面的等号成立,也就是得到了强对偶性。
使得上面的等号成立,也就是得到了强对偶性。
注意前面的分析中我们并没有提到 SCQ,那么 SCQ 是如何保证强对偶性的呢?注意 SCQ 要求存在 ![[公式]](/images/download/1613377611043_85289.png) 使得
使得 ![[公式]](/images/download/1613377611074_22987.png) ,这也就意味着
,这也就意味着 ![[公式]](/images/download/1613377611111_40879.png) 在
在 ![[公式]](/images/download/1613377611140_99796.png) 半平面上有点,因此如果支撑超平面存在的话,就一定不是垂直的。
半平面上有点,因此如果支撑超平面存在的话,就一定不是垂直的。
但这又引出另一个问题,那就是支撑超平面一定存在吗?答案是一定存在,这是由原问题的凸性质决定的。为了证明这一点,我们可以引入一个类似于 epigraph 的概念:
![[公式]](/images/download/1613377611176_39496.png)
由于原优化问题为凸的,可以应用定义证明集合 ![[公式]](/images/download/1613377611296_75553.png) 也是凸的,同时
也是凸的,同时 ![[公式]](/images/download/1613377611322_37260.png) ,那么集合
,那么集合 ![[公式]](/images/download/1613377611365_38148.png) 在
在 ![[公式]](/images/download/1613377611503_66762.png) 点就一定存在一个支撑超平面。又由 SCQ 可知这个支撑超平面一定不是竖直的,因此就可以得到强对偶性了。
点就一定存在一个支撑超平面。又由 SCQ 可知这个支撑超平面一定不是竖直的,因此就可以得到强对偶性了。
注:![[公式]](/images/download/1613377611537_43939.png) 也成立。
也成立。
4. 广义不等式约束与SDP
前面讨论拉格朗日函数的时候都只考虑了标量函数,如果约束函数为广义不等式,也即
![[公式]](/images/download/1613377611590_51648.png)
那么他的拉格朗日函数就是
![[公式]](/images/download/1613377611677_51159.png)
对偶函数就是
![[公式]](/images/download/1613377611758_87184.png)
其同样满足 ![[公式]](/images/download/1613377611826_11326.png) 。对偶问题为
。对偶问题为
![[公式]](/images/download/1613377611886_84694.png)
强对偶性以及 Slater's Condition 是类似的。
对于 SDP 问题
![[公式]](/images/download/1613377611986_35062.png)
拉格朗日函数就是
![[公式]](/images/download/1613377612062_97562.png)
对偶函数为
![[公式]](/images/download/1613377612140_76230.png)
对偶问题就是
![[公式]](/images/download/1613377612237_20731.png)
强对偶性以及 Slater's Condition 是类似的。
5. 对偶问题的强对偶性与可行性
注意我们说强对偶性需要严格满足不等式约束(也即最优解需要满足 ![[公式]](/images/download/1613377612320_45421.png) 而不能是
而不能是 ![[公式]](/images/download/1613377612360_62182.png) ),但如果存在线性不等式约束,则可以取到等号(也即
),但如果存在线性不等式约束,则可以取到等号(也即 ![[公式]](/images/download/1613377612424_81109.png) )。这就会出现下面的现象:
)。这就会出现下面的现象:
- 对于 LP 问题,由于约束是线性的,因此强对偶性只要求有可行解,而不要求 strictly feasible;
- 对于其他问题,若存在非线性约束,比如 SOCP/SDP 问题,如果想要满足强对偶性,就需要满足 strictly feasible,这就会出现两种情况:1)问题本身的可行域不可能满足 strictly feasible,那么就达不到强对偶性,于是
![[公式]](/images/download/1613377612459_84857.png) ;2)问题可行域满足 strictly feasible,但是由于最优解达不到(比如
;2)问题可行域满足 strictly feasible,但是由于最优解达不到(比如 ![[公式]](/images/download/1613377612495_99197.png) ),那么此时原问题和对偶问题仍满足强队偶性,但是原问题最优解达不到,而对偶问题则可以达到。
),那么此时原问题和对偶问题仍满足强队偶性,但是原问题最优解达不到,而对偶问题则可以达到。




1. 拉格朗日函数
考虑凸优化问题
![[公式]](/images/download/1613377606198_37693.png)
假设 ![[公式]](/images/download/1613377606557_69420.png) ,定义域为
,定义域为 ![[公式]](/images/download/1613377606592_63545.png) ,最优解为
,最优解为 ![[公式]](/images/download/1613377606625_49218.png) 。
。
我们定义拉格朗日函数(Lagrangian) 为 ![[公式]](/images/download/1613377606670_13171.png) ,
,![[公式]](/images/download/1613377606713_89503.png)
![[公式]](/images/download/1613377606755_57529.png)
再取下确界得到拉格朗日对偶函数(Lagrange dual function) ![[公式]](/images/download/1613377606838_43630.png)
![[公式]](/images/download/1613377606875_88205.png)
这个拉格朗日对偶函数可不得了啦!他有两个很重要的性质:
![[公式]](/images/download/1613377606944_64495.png) 是凹函数(不论原问题是否为凸问题)
是凹函数(不论原问题是否为凸问题)- 如果
![[公式]](/images/download/1613377606979_12105.png) ,那么
,那么 ![[公式]](/images/download/1613377607016_72455.png) (对任意
(对任意 ![[公式]](/images/download/1613377607050_37068.png) 都成立)
都成立)
Remarks:上面两个性质为什么重要呢?首先由于 ![[公式]](/images/download/1613377607098_33352.png) ,这可以给出原问题最优解的一个不平凡下界,这意味着如果原问题很难求解的时候,我们可以转变思路,求解一个新的优化问题:
,这可以给出原问题最优解的一个不平凡下界,这意味着如果原问题很难求解的时候,我们可以转变思路,求解一个新的优化问题:
![[公式]](/images/download/1613377607136_16340.png)
另一方面,由于不论原函数是否为凸优化问题,新的问题都是凸的,因此可以方便求解。下面举几个例子。
例子 1:原问题为
![[公式]](/images/download/1613377607199_37887.png)
那么可以很容易得到拉格朗日函数为 ![[公式]](/images/download/1613377607268_34516.png) ,对偶函数为
,对偶函数为 ![[公式]](/images/download/1613377607319_67732.png) ,也即
,也即
![[公式]](/images/download/1613377607379_18419.png) 。
。
例子 2:标准形式的线性规划(LP)
![[公式]](/images/download/1613377607410_88273.png)
按照定义容易得到对偶问题为
![[公式]](/images/download/1613377607473_17048.png)
例子 3:原问题为最小化范数
![[公式]](/images/download/1613377607540_20113.png)
对偶函数为
![[公式]](/images/download/1613377607594_84784.png)
这个推导过程中用到了共轭函数的知识。实际上上面三个例子都是线性等式约束,这种情况下,我们应用定义推导过程中可以很容易联想到共轭函数。(实际上加上线性不等式约束也可以)
例子 4:(原问题非凸)考虑 Two-way partitioning (不知道怎么翻译了...)
![[公式]](/images/download/1613377607682_95907.png)
对偶函数为
![[公式]](/images/download/1613377607751_78961.png)
于是可以给出原问题最优解的下界为 ![[公式]](/images/download/1613377607860_19930.png) if
if ![[公式]](/images/download/1613377607897_95387.png) 。这个下界是不平凡的,比如可以取
。这个下界是不平凡的,比如可以取 ![[公式]](/images/download/1613377607937_30840.png) ,可以给出
,可以给出 ![[公式]](/images/download/1613377607983_55086.png) 。
。
2. 对偶问题
上面已经多次提到对偶问题(Lagrange dual problem) 了
![[公式]](/images/download/1613377608026_54219.png)
假如对偶问题的最优解为 ![[公式]](/images/download/1613377608089_89994.png) ,那么我们有
,那么我们有 ![[公式]](/images/download/1613377608134_88076.png) 。
。
现在我们当然想知道什么情况下可以取等号,也即 ![[公式]](/images/download/1613377608166_40439.png) ,此时我们只需要求解对偶问题就可以获得原问题的最优解了。在此之前,我们先引入两个概念:强对偶和弱对偶。
,此时我们只需要求解对偶问题就可以获得原问题的最优解了。在此之前,我们先引入两个概念:强对偶和弱对偶。
弱对偶(weak duality):满足 ![[公式]](/images/download/1613377608204_78911.png) ,原问题不论是否为凸,弱对偶总是成立;
,原问题不论是否为凸,弱对偶总是成立;
强对偶(strong duality):满足 ![[公式]](/images/download/1613377608235_89579.png) ,强对偶并不总是成立,如果原问题为凸优化问题,一般情况下都成立。在凸优化问题中,保证强对偶成立的条件为被称为 constraint qualifications。
,强对偶并不总是成立,如果原问题为凸优化问题,一般情况下都成立。在凸优化问题中,保证强对偶成立的条件为被称为 constraint qualifications。
有很多种不同的 constraint qualifications,常用到的一种为 Slater’s constraint qualification(SCQ),其表述为
SCQ:对于凸优化问题如果存在可行解
,使得
那么就能保证强对偶性。
Remarks:
- 由于存在线性等式约束,因此实际定义域可能不存在内点,可以将这一条件放松为相对内点
![[公式]](/images/download/1613377608432_25011.png) ;
; - 如果不等式约束中存在线性不等式,那么他也不必严格小于0。也即如果
![[公式]](/images/download/1613377608463_26788.png) ,则只需要满足
,则只需要满足 ![[公式]](/images/download/1613377608503_53409.png) 即可。
即可。
下面再举几个例子,看一看他们的 SCQ 条件是什么。
例子 1:还是考虑线性规划(LP) 或者二次规划(QP)
![[公式]](/images/download/1613377608536_61744.png)
那么根据 SCQ 可以得到,如果想得到强对偶性,应该有 ![[公式]](/images/download/1613377608615_22478.png) 。
。
例子 2:(原问题非凸) Trust Region Methods
![[公式]](/images/download/1613377608656_90642.png)
其中 ![[公式]](/images/download/1613377608720_97067.png) ,因此原问题不是凸的。他的对偶函数就是
,因此原问题不是凸的。他的对偶函数就是
![[公式]](/images/download/1613377608751_60342.png)
注意如果不满足 ![[公式]](/images/download/1613377608863_71415.png) 或
或 ![[公式]](/images/download/1613377608898_59475.png) ,则
,则 ![[公式]](/images/download/1613377608932_76291.png) 。那么就可以得到对偶问题为
。那么就可以得到对偶问题为
![[公式]](/images/download/1613377608963_13585.png)
也可以等价转换为 SDP
![[公式]](/images/download/1613377609063_86018.png)
Remarks:这里用到了舒尔补(Schur complement)的知识。考虑矩阵其中
。那么有以下及条性质:
![[公式]](/images/download/1613377609222_39247.png)
- 若
![[公式]](/images/download/1613377609263_85887.png) ,则
,则 ![[公式]](/images/download/1613377609295_67997.png)
![[公式]](/images/download/1613377609335_33548.png)
关于第 3 条中的第二个要求 ![[公式]](/images/download/1613377609391_40198.png) ,对
,对 ![[公式]](/images/download/1613377609428_74824.png) 进行奇异值分解,有
进行奇异值分解,有 ![[公式]](/images/download/1613377609454_50699.png) ,那么我们对任意
,那么我们对任意 ![[公式]](/images/download/1613377609490_57255.png) ,有
,有 ![[公式]](/images/download/1613377609519_71702.png) ,而
,而 ![[公式]](/images/download/1613377609575_99337.png) 实际上就是向
实际上就是向 ![[公式]](/images/download/1613377609609_20848.png) 的投影矩阵,因此就要求
的投影矩阵,因此就要求 ![[公式]](/images/download/1613377609677_98194.png) 。
。
3. SCQ 几何解释
前面给出的是 SCQ 的代数描述,那么如何证明呢?另外如何从几何角度直观理解呢?
首先我们可以考虑最简单的优化问题
![[公式]](/images/download/1613377609716_83721.png)
定义集合 ![[公式]](/images/download/1613377609790_40031.png) ,那么对偶函数为
,那么对偶函数为
![[公式]](/images/download/1613377609843_63551.png)
如果我们画出下面这张图,阴影部分就是可行区域 ![[公式]](/images/download/1613377609918_78189.png) ,而
,而 ![[公式]](/images/download/1613377609948_56593.png) 则正好定义了一个支撑超平面,
则正好定义了一个支撑超平面,![[公式]](/images/download/1613377610002_69750.png) 就等于
就等于 ![[公式]](/images/download/1613377610045_87114.png) 轴的交点。通过取不同的
轴的交点。通过取不同的 ![[公式]](/images/download/1613377610075_14004.png) 我们就可以得到不同的支撑超平面,也可以得到不同的
我们就可以得到不同的支撑超平面,也可以得到不同的 ![[公式]](/images/download/1613377610106_73756.png) ,最终会有某一个
,最终会有某一个 ![[公式]](/images/download/1613377610136_12046.png) 对应的是
对应的是 ![[公式]](/images/download/1613377610167_44231.png) 。还需要注意这里的支撑超平面永远不可能是竖直的。
。还需要注意这里的支撑超平面永远不可能是竖直的。


那么 ![[公式]](/images/download/1613377610290_32358.png) 体现在哪个点呢?由于对于原优化问题,我们有
体现在哪个点呢?由于对于原优化问题,我们有 ![[公式]](/images/download/1613377610323_83633.png) ,因此体现在这个图里面就是
,因此体现在这个图里面就是 ![[公式]](/images/download/1613377610361_69158.png) ,也就是上面左图当中的红色区域,而
,也就是上面左图当中的红色区域,而 ![[公式]](/images/download/1613377610390_98350.png) 。
。
理解了这张图,我们现在开始证明两件事:
- 证明弱对偶性,也即
![[公式]](/images/download/1613377610431_82168.png) ;
; - 证明强对偶性条件 SCQ。
注:在此之前,我们不妨加入等式约束,也即 ![[公式]](/images/download/1613377610472_63424.png) 。
。
弱对偶性的证明:我们有 ![[公式]](/images/download/1613377610533_99687.png)
![[公式]](/images/download/1613377610567_56890.png)
强对偶性条件 SCQ 的证明:由 ![[公式]](/images/download/1613377610698_13284.png) 可以得到
可以得到
![[公式]](/images/download/1613377610755_99304.png)
这实际上定义了 ![[公式]](/images/download/1613377610820_55605.png) 的一个超平面。特别的有
的一个超平面。特别的有 ![[公式]](/images/download/1613377610846_81934.png) ,因此也有
,因此也有
![[公式]](/images/download/1613377610886_85421.png)
这个不等式可以自然地导出弱对偶性,当“=”成立时则可以导出强对偶性。那么什么时候取等号呢?点 ![[公式]](/images/download/1613377610940_24454.png) 为支撑点的时候!也就是说
为支撑点的时候!也就是说
如果在边界点处存在一个非竖直的支撑超平面,那么我们就可以找到
使得上面的等号成立,也就是得到了强对偶性。
注意前面的分析中我们并没有提到 SCQ,那么 SCQ 是如何保证强对偶性的呢?注意 SCQ 要求存在 ![[公式]](/images/download/1613377611043_85289.png) 使得
使得 ![[公式]](/images/download/1613377611074_22987.png) ,这也就意味着
,这也就意味着 ![[公式]](/images/download/1613377611111_40879.png) 在
在 ![[公式]](/images/download/1613377611140_99796.png) 半平面上有点,因此如果支撑超平面存在的话,就一定不是垂直的。
半平面上有点,因此如果支撑超平面存在的话,就一定不是垂直的。
但这又引出另一个问题,那就是支撑超平面一定存在吗?答案是一定存在,这是由原问题的凸性质决定的。为了证明这一点,我们可以引入一个类似于 epigraph 的概念:
![[公式]](/images/download/1613377611176_39496.png)
由于原优化问题为凸的,可以应用定义证明集合 ![[公式]](/images/download/1613377611296_75553.png) 也是凸的,同时
也是凸的,同时 ![[公式]](/images/download/1613377611322_37260.png) ,那么集合
,那么集合 ![[公式]](/images/download/1613377611365_38148.png) 在
在 ![[公式]](/images/download/1613377611503_66762.png) 点就一定存在一个支撑超平面。又由 SCQ 可知这个支撑超平面一定不是竖直的,因此就可以得到强对偶性了。
点就一定存在一个支撑超平面。又由 SCQ 可知这个支撑超平面一定不是竖直的,因此就可以得到强对偶性了。
注:![[公式]](/images/download/1613377611537_43939.png) 也成立。
也成立。
4. 广义不等式约束与SDP
前面讨论拉格朗日函数的时候都只考虑了标量函数,如果约束函数为广义不等式,也即
![[公式]](/images/download/1613377611590_51648.png)
那么他的拉格朗日函数就是
![[公式]](/images/download/1613377611677_51159.png)
对偶函数就是
![[公式]](/images/download/1613377611758_87184.png)
其同样满足 ![[公式]](/images/download/1613377611826_11326.png) 。对偶问题为
。对偶问题为
![[公式]](/images/download/1613377611886_84694.png)
强对偶性以及 Slater's Condition 是类似的。
对于 SDP 问题
![[公式]](/images/download/1613377611986_35062.png)
拉格朗日函数就是
![[公式]](/images/download/1613377612062_97562.png)
对偶函数为
![[公式]](/images/download/1613377612140_76230.png)
对偶问题就是
![[公式]](/images/download/1613377612237_20731.png)
强对偶性以及 Slater's Condition 是类似的。
5. 对偶问题的强对偶性与可行性
注意我们说强对偶性需要严格满足不等式约束(也即最优解需要满足 ![[公式]](/images/download/1613377612320_45421.png) 而不能是
而不能是 ![[公式]](/images/download/1613377612360_62182.png) ),但如果存在线性不等式约束,则可以取到等号(也即
),但如果存在线性不等式约束,则可以取到等号(也即 ![[公式]](/images/download/1613377612424_81109.png) )。这就会出现下面的现象:
)。这就会出现下面的现象:
- 对于 LP 问题,由于约束是线性的,因此强对偶性只要求有可行解,而不要求 strictly feasible;
- 对于其他问题,若存在非线性约束,比如 SOCP/SDP 问题,如果想要满足强对偶性,就需要满足 strictly feasible,这就会出现两种情况:1)问题本身的可行域不可能满足 strictly feasible,那么就达不到强对偶性,于是
![[公式]](/images/download/1613377612459_84857.png) ;2)问题可行域满足 strictly feasible,但是由于最优解达不到(比如
;2)问题可行域满足 strictly feasible,但是由于最优解达不到(比如 ![[公式]](/images/download/1613377612495_99197.png) ),那么此时原问题和对偶问题仍满足强队偶性,但是原问题最优解达不到,而对偶问题则可以达到。
),那么此时原问题和对偶问题仍满足强队偶性,但是原问题最优解达不到,而对偶问题则可以达到。




Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=699

Best Last Month

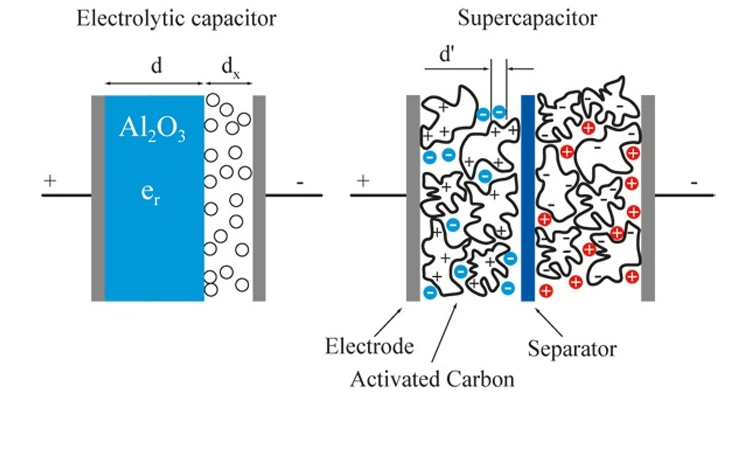
supercapacitor-battery materials for fast electrochemical charge storage