News Message
石墨烯导电性能优异的物理分析
- by wittx 2020-07-03
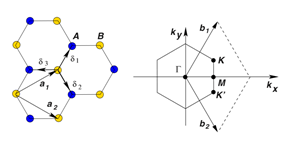
石墨烯导电性强,不仅仅是因为零能隙,更重要的是在零能隙的这些点上电子性质的独特性。当我们谈论一个材料的电子学特性的时候也需要关注他的能带分布。什么是能带分布,首先我们要来看石墨烯的晶体结构与倒格子,所谓倒格子是与晶格空间相对应傅里叶变换出来的波矢空间,也可以说是动量空间,因为![[公式]](/images/download/1593776828487_21561.png) ,这个空间很重要所有关于石墨烯电子运动的叙述都要在此空间中展开
,这个空间很重要所有关于石墨烯电子运动的叙述都要在此空间中展开
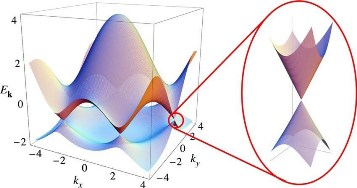
石墨烯的能带分布是靠紧束缚模型算出来的。什么是紧束缚模型?在紧束缚模型中电子想要跃迁到其他地方,需要脱离原子的势场,所以我们将在一个原子附近的电子看作受该原子势场的作用为主,其他原子势场的作用看成微扰,从而可以得到能带分布。于是我们就有这样一张关于石墨烯的能带分布图
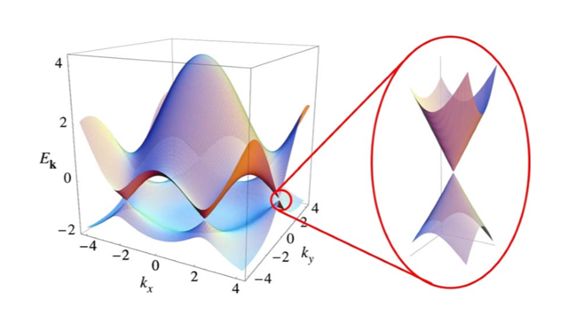
![[公式]](/images/download/1593776830151_29546.png) 的色散关系(能量与波矢的关系)
的色散关系(能量与波矢的关系)
![[公式]](/images/download/1593776830269_54801.png)
我们可以看出来在K,K'点附近色散关系是近似线性的,这说明什么,在量子力学中动量与波矢差得只是一个约化普朗克常量,也就等效于动量与能量的关系为线性,这也就表明电子的速度为常量,并不受动量与动能的影响,我们把![[公式]](/images/download/1593776830426_49356.png) 定义为费米速度
定义为费米速度![[公式]](/images/download/1593776830533_95498.png) 。
。
在描述电子运动的时候,我们往往把一个在晶格内运动的电子,等效为一个在自由空间中运动的电子,所以我们可以引入一个有效质量的概念,将晶体中的场对于电子的影响等效于自由空间运动的电子的质量![[公式]](/images/download/1593776830707_43778.png) ,由于色散关系为线性,且在能量为零的点对称,导致E(k)在K点不连续,导致二阶导数无穷大,所以电子的有效质量为零。
,由于色散关系为线性,且在能量为零的点对称,导致E(k)在K点不连续,导致二阶导数无穷大,所以电子的有效质量为零。
这种情况下,我们用薛定谔方程来描述粒子的运动已经无效了,我们需要运用引入了相对论效应的狄拉克方程来描述。事实上当我们将电子算符在K,K’进行傅里叶展开,代入哈密顿量之后,我们可以得到一个与二维的无质量电子的狄拉克方程近似的方程
![[公式]](/images/download/1593776830851_88726.png)
通过上面的公式,我们可以在K附近可以得到波函数在K的分量 为
![[公式]](/images/download/1593776830999_41101.png)
在K'的分量为
![[公式]](/images/download/1593776831149_99214.png)
我们可以看到我们将M作为原点,可以看到两个分量的方向是轴对称的,并且相位差为![[公式]](/images/download/1593776831328_84223.png) ,粒子波函数在两个波矢方向的分量可以等效为一组自旋量。对于自旋量与动量的关系,我们可以引入螺旋度的概念,既动量算子对于自旋方向的投影,螺旋度的算子定义为:
,粒子波函数在两个波矢方向的分量可以等效为一组自旋量。对于自旋量与动量的关系,我们可以引入螺旋度的概念,既动量算子对于自旋方向的投影,螺旋度的算子定义为:![[公式]](/images/download/1593776831436_95808.png) 。由于自旋量在物理实质上是粒子的波函数的动量分量,所以我们很容易得到其螺旋度为
。由于自旋量在物理实质上是粒子的波函数的动量分量,所以我们很容易得到其螺旋度为![[公式]](/images/download/1593776831555_55046.png) 。这与狄拉克方程中所描述的无质量的自旋为
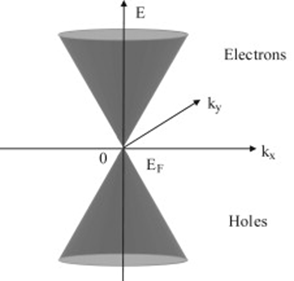
。这与狄拉克方程中所描述的无质量的自旋为![[公式]](/images/download/1593776831675_36201.png) 的电子相似,狄拉克方程中,电子自旋方向只会与动量方向相同(正粒子),或与动量方向相反(反粒子),而在石墨烯中K,K'附近的电子就对应的是正粒子(螺旋量,能量为正),空穴对应的是反粒子(螺旋量,能量为负)。这样电子与空穴与狄拉克方程所描述自由空间中无质量的两种状态的电子等效,所以我们可以把石墨烯狄拉克的空穴与电子称为狄拉克费米子,K,K'被称为狄拉克点。
的电子相似,狄拉克方程中,电子自旋方向只会与动量方向相同(正粒子),或与动量方向相反(反粒子),而在石墨烯中K,K'附近的电子就对应的是正粒子(螺旋量,能量为正),空穴对应的是反粒子(螺旋量,能量为负)。这样电子与空穴与狄拉克方程所描述自由空间中无质量的两种状态的电子等效,所以我们可以把石墨烯狄拉克的空穴与电子称为狄拉克费米子,K,K'被称为狄拉克点。
关于石墨烯非常高的电子迁移率的原因也是由于狄拉克点的存在,由于量子隧穿效应的影响,电子有概率穿过高于自身能量的势场,对于如下图的势场,通过计算我们可以得到狄拉克费米子的隧穿概率
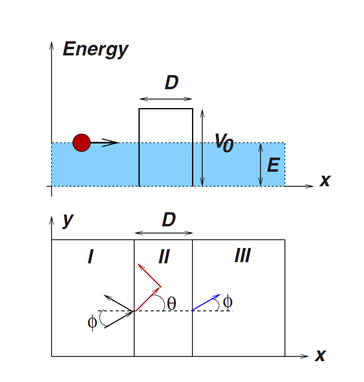
![[公式]](/images/download/1593776832663_99755.png)
当![[公式]](/images/download/1593776832792_85617.png) 时隧穿概率为1,这只有狄拉克费米子才有的性质,对于非相对论条件下的电子无用,正是因为在粒子在石墨烯中可以完全隧穿,使得石墨烯中的空穴与电子可以拥有非常长的自由程。也是因此石墨烯的电子运动几乎不受声子碰撞的影响,这使得电子运动受温度的影响非常小,同时在强场下电子的迁移率也保持得比一般材料好。
时隧穿概率为1,这只有狄拉克费米子才有的性质,对于非相对论条件下的电子无用,正是因为在粒子在石墨烯中可以完全隧穿,使得石墨烯中的空穴与电子可以拥有非常长的自由程。也是因此石墨烯的电子运动几乎不受声子碰撞的影响,这使得电子运动受温度的影响非常小,同时在强场下电子的迁移率也保持得比一般材料好。
综上所述,石墨烯良好的电子学性质并不是因为其“半金属”性,而是由于狄拉克点的存在。
1:零能隙
石墨烯是semimetal,它应该不是半导体。(但是在特殊情况下能带结构又有点像)
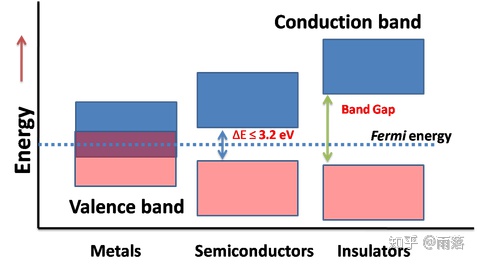
Figure 1: band diagram of Metal, Semiconductors, and Insulators [1] 金属是导带和价带重合,有自由移动的电子。
半导体是有适中的能带间隙。
绝缘体是有很大的能带间隙。
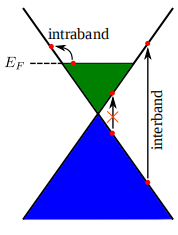
Figure 2: Band structure of graphene [2] 一般情况下,石墨烯的导带和价带是连接的,那个点叫Dirac point,在小于1eV的范围内这个band structure是线性的。(我记得在不记得哪篇文献上看到的这个数据)
我的理解是,在导带上的电子是可以自由移动的电子。
石墨烯的导电性好,是源于它的结构。
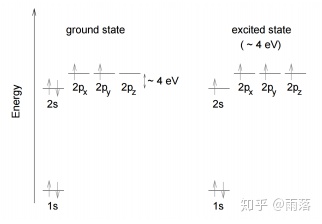
Figure 3: Electronic configuration of carbon [3] 在激发态的情况下,有个2S上的电子跑2P上了,然后三个电子和周围的碳原子配对,剩下一个自由移动的电子。六边形,每个碳原子和周围的3个碳原子连接。
单层石墨烯导电性强还有个别的原因。
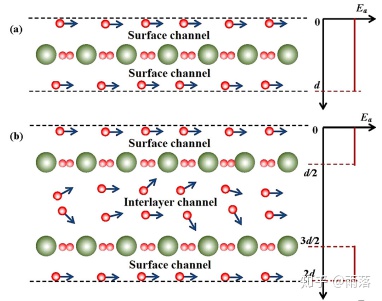
Figure 4. Schematic diagram of the transport channel of monolayer graphene and bilayer graphene [4] 单层石墨烯因为没有层与层之间的散射,所以导电性会很好,导电性会随着层数的增加逐渐衰减[4]。
转自:https://www.zhihu.com/question/24285104/answer/43627219
石墨烯导电性强,不仅仅是因为零能隙,更重要的是在零能隙的这些点上电子性质的独特性。当我们谈论一个材料的电子学特性的时候也需要关注他的能带分布。什么是能带分布,首先我们要来看石墨烯的晶体结构与倒格子,所谓倒格子是与晶格空间相对应傅里叶变换出来的波矢空间,也可以说是动量空间,因为![[公式]](/images/download/1593776828487_21561.png) ,这个空间很重要所有关于石墨烯电子运动的叙述都要在此空间中展开
,这个空间很重要所有关于石墨烯电子运动的叙述都要在此空间中展开

石墨烯的能带分布是靠紧束缚模型算出来的。什么是紧束缚模型?在紧束缚模型中电子想要跃迁到其他地方,需要脱离原子的势场,所以我们将在一个原子附近的电子看作受该原子势场的作用为主,其他原子势场的作用看成微扰,从而可以得到能带分布。于是我们就有这样一张关于石墨烯的能带分布图

![[公式]](/images/download/1593776830151_29546.png) 的色散关系(能量与波矢的关系)
的色散关系(能量与波矢的关系)![[公式]](/images/download/1593776830269_54801.png)
我们可以看出来在K,K'点附近色散关系是近似线性的,这说明什么,在量子力学中动量与波矢差得只是一个约化普朗克常量,也就等效于动量与能量的关系为线性,这也就表明电子的速度为常量,并不受动量与动能的影响,我们把
![[公式]](/images/download/1593776830426_49356.png) 定义为费米速度
定义为费米速度![[公式]](/images/download/1593776830533_95498.png) 。
。在描述电子运动的时候,我们往往把一个在晶格内运动的电子,等效为一个在自由空间中运动的电子,所以我们可以引入一个有效质量的概念,将晶体中的场对于电子的影响等效于自由空间运动的电子的质量
![[公式]](/images/download/1593776830707_43778.png) ,由于色散关系为线性,且在能量为零的点对称,导致E(k)在K点不连续,导致二阶导数无穷大,所以电子的有效质量为零。
,由于色散关系为线性,且在能量为零的点对称,导致E(k)在K点不连续,导致二阶导数无穷大,所以电子的有效质量为零。这种情况下,我们用薛定谔方程来描述粒子的运动已经无效了,我们需要运用引入了相对论效应的狄拉克方程来描述。事实上当我们将电子算符在K,K’进行傅里叶展开,代入哈密顿量之后,我们可以得到一个与二维的无质量电子的狄拉克方程近似的方程
![[公式]](/images/download/1593776830851_88726.png)
通过上面的公式,我们可以在K附近可以得到波函数在K的分量 为
![[公式]](/images/download/1593776830999_41101.png)
在K'的分量为
![[公式]](/images/download/1593776831149_99214.png)
我们可以看到我们将M作为原点,可以看到两个分量的方向是轴对称的,并且相位差为
![[公式]](/images/download/1593776831328_84223.png) ,粒子波函数在两个波矢方向的分量可以等效为一组自旋量。对于自旋量与动量的关系,我们可以引入螺旋度的概念,既动量算子对于自旋方向的投影,螺旋度的算子定义为:
,粒子波函数在两个波矢方向的分量可以等效为一组自旋量。对于自旋量与动量的关系,我们可以引入螺旋度的概念,既动量算子对于自旋方向的投影,螺旋度的算子定义为:![[公式]](/images/download/1593776831436_95808.png) 。由于自旋量在物理实质上是粒子的波函数的动量分量,所以我们很容易得到其螺旋度为
。由于自旋量在物理实质上是粒子的波函数的动量分量,所以我们很容易得到其螺旋度为![[公式]](/images/download/1593776831555_55046.png) 。这与狄拉克方程中所描述的无质量的自旋为
。这与狄拉克方程中所描述的无质量的自旋为![[公式]](/images/download/1593776831675_36201.png) 的电子相似,狄拉克方程中,电子自旋方向只会与动量方向相同(正粒子),或与动量方向相反(反粒子),而在石墨烯中K,K'附近的电子就对应的是正粒子(螺旋量,能量为正),空穴对应的是反粒子(螺旋量,能量为负)。这样电子与空穴与狄拉克方程所描述自由空间中无质量的两种状态的电子等效,所以我们可以把石墨烯狄拉克的空穴与电子称为狄拉克费米子,K,K'被称为狄拉克点。
的电子相似,狄拉克方程中,电子自旋方向只会与动量方向相同(正粒子),或与动量方向相反(反粒子),而在石墨烯中K,K'附近的电子就对应的是正粒子(螺旋量,能量为正),空穴对应的是反粒子(螺旋量,能量为负)。这样电子与空穴与狄拉克方程所描述自由空间中无质量的两种状态的电子等效,所以我们可以把石墨烯狄拉克的空穴与电子称为狄拉克费米子,K,K'被称为狄拉克点。
关于石墨烯非常高的电子迁移率的原因也是由于狄拉克点的存在,由于量子隧穿效应的影响,电子有概率穿过高于自身能量的势场,对于如下图的势场,通过计算我们可以得到狄拉克费米子的隧穿概率

![[公式]](/images/download/1593776832663_99755.png)
当
![[公式]](/images/download/1593776832792_85617.png) 时隧穿概率为1,这只有狄拉克费米子才有的性质,对于非相对论条件下的电子无用,正是因为在粒子在石墨烯中可以完全隧穿,使得石墨烯中的空穴与电子可以拥有非常长的自由程。也是因此石墨烯的电子运动几乎不受声子碰撞的影响,这使得电子运动受温度的影响非常小,同时在强场下电子的迁移率也保持得比一般材料好。
时隧穿概率为1,这只有狄拉克费米子才有的性质,对于非相对论条件下的电子无用,正是因为在粒子在石墨烯中可以完全隧穿,使得石墨烯中的空穴与电子可以拥有非常长的自由程。也是因此石墨烯的电子运动几乎不受声子碰撞的影响,这使得电子运动受温度的影响非常小,同时在强场下电子的迁移率也保持得比一般材料好。综上所述,石墨烯良好的电子学性质并不是因为其“半金属”性,而是由于狄拉克点的存在。
石墨烯是semimetal,它应该不是半导体。(但是在特殊情况下能带结构又有点像)

金属是导带和价带重合,有自由移动的电子。
半导体是有适中的能带间隙。
绝缘体是有很大的能带间隙。

一般情况下,石墨烯的导带和价带是连接的,那个点叫Dirac point,在小于1eV的范围内这个band structure是线性的。(我记得在不记得哪篇文献上看到的这个数据)
我的理解是,在导带上的电子是可以自由移动的电子。
石墨烯的导电性好,是源于它的结构。

在激发态的情况下,有个2S上的电子跑2P上了,然后三个电子和周围的碳原子配对,剩下一个自由移动的电子。六边形,每个碳原子和周围的3个碳原子连接。
单层石墨烯导电性强还有个别的原因。

单层石墨烯因为没有层与层之间的散射,所以导电性会很好,导电性会随着层数的增加逐渐衰减[4]。
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=301




.jpg)
